孩子升到小学高年级后,数学成绩一路下滑,刷题只会加重负担,孩子产生抗拒心理;孩子听老师讲解立马恍然大悟,但自己做的时候永远找不到思路;家长陪孩子做应用题,第一时间用X/Y方程求解,但孩子年龄小,讲解他又不明白;孩子觉得数学都是公式数字,很枯燥,提不起兴趣。
在小学阶段会出现以上问题,往往是因为从具体事物到抽象思维这关过不好。没有办法理解为什么这些符号、数字就能够进行运算?它们是怎么来的?又为什么这么算??其实孩子的思维认知发展有着基本的规律。孩子在小学一二年级的时候,首先出现的是非常具体的形象思维。你会看到学习内容上,语文就是认字、识词、造句,数学就是看着实物数数,加减乘除,都是认识具体事物的方法。
从三年级开始,孩子的思维要开始进入另一个阶段,完成从具体的事物到抽象概念、公式的转变。所以有一些家长会发现,3、4年级的孩子数学成绩会突然之间下降,学习进度变慢,而家长也多将此错误地归结为孩子学习态度出现了问题。
实际上是因为在具体思维阶段没有做足功课,就让孩子直接进入充满抽象的符号、公式的世界,数学就会变成一门看不见摸不着的学科了,他们会迷惑,会有挫败感,甚至产生厌学情绪,从而形成恶性循环。?因此,如何帮助孩子建立从具体思维到抽象思维过渡的桥梁,就是解决以上问题的关键。
要如何理解CPA的这个过程呢?首先回忆一下我们小时候一开始接触数学,靠数数来计算不会是直接1、2、3……或者直接就学习1+1=2。老师家长都会告诉我们前面有1个苹果、2个苹果;1只乌龟加上另一只乌龟等于两只乌龟,诸如此类。
总的来说就是通过非常具体的事物,让我们对数量的增加或者减少有最基础的认知,这就是C(具象化)。
紧接着,当我们再被问到这个问题的时候,我们脑海里就会想象出有两只乌龟放在一起,这就是P(形象化)。
在这之后,我们看到应用题文字的时候“有一只小狗,又来了另一只小狗,一共是多少只小狗“,这时我们在纸上写下「1+1=2」,这就是A(抽象化)。?实际上,这种从具象到形象再到抽象的学习过程(从C到P到A),我们国内也是有的,比如用线段图、表格图来使问题形象化,
这就会容易让学生形成两种极端,一种就是很多人口中说的“牛娃”,本来他的思维发展就比较快,即使不用通过中间的P,也能直接从C到A,我国的数学教育方式对他们来说完全没有难度,并且也凭着这样的强化将直接抽象的能力变得越来越熟练。
??如何才能让孩子转变自己的思考方式,学会用图像化思维做数学题呢?下面我们来看一道题。
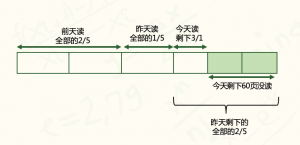
这道题对于刚刚学会分数的孩子可能会很头晕。搞不清究竟是什么数量关系,自然也无从下手,家长们也许比较习惯用X求解。但对于还没接触到方程的孩子来说,可能会无法理解,家长讲解起来也抓狂。?但从模型图上看,就能很好地理解到今天剩下的60页就占昨天剩下的2/3,因此就可以得出,60÷(1-1/3)=90页。这90页就是昨天剩下的页数,占到了全部的2/5,因此可得90÷(1-2/5-1/5)=225页。
可能有的家长会认为,只要等到孩子学会代数,引入方程就简单快捷多了,这样解题不是更复杂化了吗?完全没有必要呀。?实际上,画模型图可以帮助孩子真正读懂题目。在画图时,孩子心中必须一直要有数量的概念在的,数量间的关系是如何对比,是怎么增加怎么减少的,都要做到心中有数,这对培养孩子的数感很有帮助,对题目自然也会理解得很透彻。?同时这种方法更能培养孩子数学思维的系统性。随着高年级学习,往往一道应用题里面会藏着多个数学知识点,绘图的过程会变得非常复杂,需要在C-P-A的三个阶段中反复贯穿理解与确认,不能顾此失彼,无疑会很考验孩子对数学的整体概念,而非管中窥豹。?学好模型图可以为以后更高级的数学奠定基础。
另外,在解答数学题的时候,尽可能让孩子坚持画模型图,当P「形象化」变成自然而然发生的时候,就能内化成一种思维模式,要熟练到甚至没有画图,脑海里也能出现这样的关系模型图,再面对高阶的抽象思维的时候,一切都了然于胸。







