比例的认识
板块一:我会学
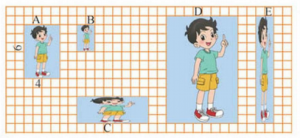
- 从图中,我能找到与图A像的是图( )和图( )。在相像的两幅图中,其中:图A与图( )长与长的比是( ):( ),宽与宽的比是( ):( );图A与图( )长与长的比是( ):( ),宽与宽的比是( ):( )。
2、从图中,我能写出每幅图的长与宽的比各是多少?并能求出它们的比值。
图A:_______:________=_______
图B:_______:________=_______
图C:_______:________=_______
图D:_______:________=_______
图E:_______:________=_______
我发现,比值( )的图片像,如图( ),比值( )的图片不像,如图( )。
3、由此可见,比相等的两张图片( );而( )不相等的两张图片( )。
4、从上面的比中写出两个相等的比,如:
( ):( )=( ):( )像这样表示两个比相等的式子叫作( )。其中( )和( )是这个比例的( )项,( )和( )是这个比例的( )项。
( ):( )=( ):( ),也可以写成:=。
- 判断两个比是否相等的方法有:
①______________;②______________。
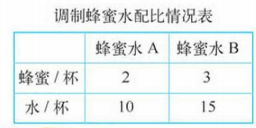
- 从表中的数据,根据比例的意义,选择喜欢的方法写比例:
( ):( )=( ):( )
( ):( )=( ):( )
= =
……
- 观察6:4=12:8的两个内项与两个外项,用算一算的方法,找一找它们的规律:
- 两个内项与两个外项的和:
________________________________;
- 两个内项与两个外项的差:
________________________________;
- 两个内项与两个外项的积:
________________________________;
- 两个内项与两个外项的商:
________________________________。
- 我发现,两个内项与两个外项的( )相等。
- 我猜测,在比例里,两个内项与两个外项的( )相等。
- 我可以再写出几个比例来进行验证:
- 所以,在比例里,两个内项的( )等于( ),这就是比例的基本性质。
- 我的延伸:=中,( )和( )是比例的外项,( )和( )是比例的( )项。如果把比例写成分数形式,比例的基本性质就是等号两端分子和分母( )相乘,积相等。
- 概念区分:上学期我们学习了“比”现在又知道了“比例”的意义。我知道了“比”和“比例”的区别与联系。
- 区别:
①意义:两个数相除又叫作两个数的( );表示两个比相等的式子叫作( )。
②项数:比有( )个项,分别是前项和后项有( )个项,分别是( )和( )。
- 联系:
比是( )的一部分。而比例是由两个比值( )的比组合而成的。
板块二:我会做
- 在括号里填上适当的数。
= =
( ):0.36=2:( )
( ):2.5=( ):100
- 根据3:9=6:18,回答:
- 如果把外项18减去6,内项9怎么变化,比例仍然成立?
- 如果内项6乘2,内项9换成哪个数,此比例仍然成立?
- 在一个比例中,两个内项互为倒数,其中一个外项是4,另一个外项是几?
- 在一个比例中,两个内项的积是最小的合数,其中一个外项是5,求另一个外项。
板块三:我能行
- 两瓶同样重的盐水,甲瓶盐水盐与水的质量比是1:8,乙瓶盐水盐与水的质量比是1:5。现将两瓶盐水倒入同一容器中,问在混合后的盐水中盐与水质量的比是多少?